01. 확률분포
표준정규분포
표준화 변환(Standardization)
: 데이터의 값들을 정규화하여 평균이 0이고 분산이 1이 되도록 변환하는 것.
Z = (X - μ) / σ → Z~N(0,1) : 표준화 변환
표준정규분포(Standard Nomal Distribution)
:평균이 0이고 분산이 1인 정규분포
| 정규화(Normalization) | 표준화(Standardization) |
| - 데이터의 범위를 특정 구간으로 맞추는 과정 - 데이터의 크기를 줄여 비교가 쉬움 - 계산 성능(효율성)을 높임 - 거리 기반 알고리즘 적용 시 성능 향상에 도움 - 변수 간 상대적인 크기 비교가 쉬워짐 |
- 데이터의 평균을 0, 표준편차를 1로 맞추는 과정 - 변수가 서로 다른 단위를 가지고 있어도, 공평한 기준에서 비교할 수 있게함 - 데이터 간 차이를 더욱 직관적으로 파악할 수 있음 |
02. 정규분포에서 표본추출하기
모집단이 정규분포를 따른 때 n개의 표본을 추출하여 구한 표본평균은 다음과 같은 정규분포를 따른다.
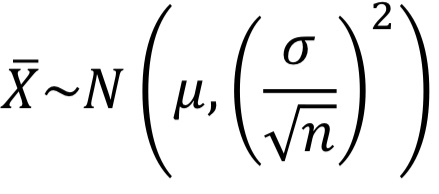
정규분포를 따르는 모집단에서 추출한 표본의 평균들은 모집단을 따라 정규분포를 띤다.
비정규분포에서 표본을 추출하면 추출한 표본의 크기가 클수록 정규분포에 가까워진다.
중심극한정리(Central Limit Theorem)
: 평균 μ와 표준편차 σ가 존재하는 임의의 분포를 모집단에서 추출한 표본의 크기 n이 증가할수록 표본평균의 분포는 평균이 μ이고, 표준편차가 σ / sqr(n) 인 정규분포를 따른다. - [수식1] 참고
추측통계학
: 모집단의 특성을 추측하는 통계학 세부 연구 분야
- 통계적 추론(statical inference) : 표본을 통해 모집단의 특성 추측
- 모수(parameter) : 알고자 하는 모집단의 특성.
- 추정량(estimator) : 모수를 알기 위해 표본을 관찰하여 얻은 특성.
- 통계적 가설 검정(test of statistical) : 표본을 통해 세운 모집단 특성의 가설 중 무엇을 채택할지 검정
표준오차(SE : Standard Error)
: 추정량의 표준편차
- 확률변수인 표본평균의 표준편차이다.
- 추정의 정밀도를 나타낸다.
- 표본의 크기가 클수록 표준오차는 감소한다.

'⚡️ 전공수업 > R' 카테고리의 다른 글
| [R통계분석] R을 활용한 확률과 통계 3 - 통계적 추론 2 (0) | 2024.12.03 |
|---|---|
| [R통계분석] R을 활용한 확률과 통계1 - 기초 확률, 확률분포1 (0) | 2024.12.03 |
| [R통계분석] R 데이터 시각화1 - ggplot2 기본 (0) | 2024.10.13 |
| [R통계분석] R 프로그래밍 - 반복문, 조건문 (0) | 2024.10.13 |
| [R통계분석] R 데이터 처리2 - 주요함수 (0) | 2024.10.12 |